Matched Filter - Baseband pulse transmission

Ask

(i) For the signal s(t) in figure , find the impulse response of matched filter
(a)s(t-T)
(b)s(T-t )
(c)s(t-2T)
(d) none of the above

(ii) For the above, find the peak value of the output of matched fillter (a)$A^2 T/4$
(b)$A^2T/2$
(c)$AT/4$
(d)$AT/2$


Answer for (i) is ( b )
Answer for (ii) is ( a )

Concept

Solution to (i)

Concept of Matched Filter

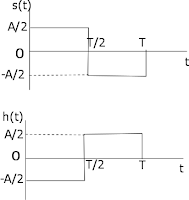
Let the Matched Filter be h(t). It should correspond to the signal s(t) as below :

Therefore, the matched filter h(t) = s(T-t). Option (b)

Solution to (ii) .

The output of the matched filter will be y(t) , which is convolution of x(t) and h(t)

y(t)  = x(t) * h(t) = $\int_{-\infty}^{\infty}h(\tau)x(t-\tau)d\tau$

To convolute two signals graphically , the following steps are summarized :

Refer the Link to watch a flash tutorial for graphical convolution :https://engineering.purdue.edu/VISE/ee438/demos/flash/convolution.html