Showing posts with label communications. Show all posts
Showing posts with label communications. Show all posts
Detection of AM signal using Envelope Detector
 |
| Ask |
An AM signal is detected using an envelope detector. The carrier frequency and modulating signal frequency are 1 MHz & 2 kHz respectively
An Appropriate value for the time constant of the envelope detector is
(a)500 micro second
(b)20 micro second
(c)0.2 micro second
(d)1 microsecond
Answer is ( )
Concept
Type Reasoning here
Superheterodyne Receiver
 |
| Ask |
A superheterodyne receiver is to operate in the frequency range 550kHz-1650kHz, intermediate frequency 450kHz
Let R=C(min)/C(max) denote required capacitance ratio of local oscillator &I denote image frequency in kHz of incoming signal.If receiver is tuned to 700kHz then
(a)R = 4.41 , I = 1600
(b)R= 2.10, I = 1150
(c)R = 3, I = 1600
(d)R =9 ,I = 1150Answer is ( )
Concept
Type Reasoning here
Modulation Basic Equations
 |
| Ask |
Find the correct match between group 1 & group 2 Group
P. $ (1+km(t)A sin(\Omega t))$
Q.$ km(t) A sin(\Omega t)$
R.$ A sin(\Omega t + k m(t))$
S. $ A sin[\Omega t + k \int (m(t))]$
Group 2
W. Phase Modulation
X. Frequency Modulation
Y. Amplitude Modulation
Z. DSB-SC Modulation
(a) P-Y , Q- Z , R- W, S-X
(b) P-Z , Q -Y, R - W, S- X
(c) P- X, Q-W,R-Y,S-Z
(d) none of above
Answer is ( a )
Concept
$ (1+km(t)A sin(\Omega t))$ - Amplitude Modulation$ km(t) A sin(\Omega t)$ - DSB-SC Modulation
$ A sin(\Omega t + k m(t))$ - Phase Modulation
$ A sin[\Omega t + k \int (m(t))]$ - Frequency Modulation
auto-correlation variance
 |
| Ask |
If the variance $\sigma_x^2$ of $d(n)= x (n) - x(n-1)$ is one-tenth the variance $\sigma_x^2 $ of a stationary zero mean discrete time signal x(n), then the normalized auto-correlation function
$\frac{R_{xx}(k) }{\sigma_x^2}$ at k = 1 is
(a) 0.95
(b) 0.90
(c) 0.10
(d) 0.05Answer is ( a )
Let's understand the definition of variance $$\sigma^2 = Var [A] $$, where A is any random process
Concept
Then , $$\sigma^2 = E [ (A-E(A))^2] $$
$ = E[(A^2 - 2AE(A) + (E(A))^2)]$
Taking Expectation E within the brackets:
$ =E[A^2] -2E[A]E[A] + (E(A))^2 $
$ = E[A^2] -(E[A])^2$
A mnemonic for the above expression is "mean of square minus square of mean"
The process is defined by :
$d(n) = x(n) - x(n-1)$
And also given that process is zero-mean.E[x(n)] =0 $\implies (E[x(n)-x(n-1)])^ 2 = 0 $
Hence,Variance of d(n) = $\sigma_d^2 = E[(x(n)-x(n-1))^2] - (E[x(n)-x(n-1)])^2$
$\sigma_d^2 = E[(x(n)-x(n-1))^2] - 0 $
$\sigma_d^2 = E[(x(n))^2 +(x(n-1))^2 - 2x(n)x(n-1)] $
$\sigma_d^2 = E[(x(n))^2] +E[(x(n-1))^2] - 2 E[x(n)x(n-1)] $
$$\sigma_d^2 = \sigma_x^2 \times \frac{1}{10}$$
The expression $ E[x(n)x(n-1)] $ is auto-correlation by lag 1.
In general , the autocorrelation function with lag k is defined by the following equation
$$R_{xx}(k) = E[x(n)x(n-k)]$$
$\sigma_x^2 \times \frac{1}{10}= \sigma_x^2 + \sigma_x^2 - 2R_{xx}(1)$
$\implies \frac{ R_{xx}(1)}{\sigma_x^2 } = 19/20 = 0.95$
Matched Filter - Baseband pulse transmission

 |
| Ask |
(a)s(t-T)
(b)s(T-t )
(c)s(t-2T)
(d) none of the above
(ii) For the above, find the peak value of the output of matched fillter (a)$A^2 T/4$
(b)$A^2T/2$
(c)$AT/4$
(d)$AT/2$
Answer for (i) is ( b )
Answer for (ii) is ( a )
Solution to (i)
Concept
Concept of Matched Filter
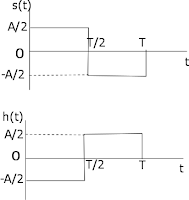
Let the Matched Filter be h(t). It should correspond to the signal s(t) as below :
Therefore, the matched filter h(t) = s(T-t). Option (b)
Solution to (ii) .
The output of the matched filter will be y(t) , which is convolution of x(t) and h(t)
y(t) = x(t) * h(t) = $\int_{-\infty}^{\infty}h(\tau)x(t-\tau)d\tau$
To convolute two signals graphically , the following steps are summarized :
Refer the Link to watch a flash tutorial for graphical convolution :https://engineering.purdue.edu/VISE/ee438/demos/flash/convolution.html
Equation Match
 |
| Ask |
Find the correct match between group 1 & group 2
Group 1
P. ${1 + km(t) A sin(\Omega t)}$
Q.$ km(t) A sin(\Omega t) $
R.$ A sin{\Omega t + k m(t)}$
S. $A sin[\Omega t + k \int (m(t))]$
Group 2
W. Phase Modulation
X. Frequency Modulation
Y. Amplitude Modulation
Z. DSB-SC Modulation
(a) P-Y , Q- Z , R- W, S-X
(b) P-Z , Q -Y, R - W, S- X
(c)P- X, Q-W,R-Y,S-Z
(d)none of above
Answer is ( a )
Concept
Type Reasoning here
Problems on LPF 1.1
 |
| Ask |
A 1kHz signal is sampled at the rate of 1.8kHz and the samples are applied to an ideal rectangular LPF with a cut-off frequency of 1.1kHz, then the output of the filter contains
(a) only 800 Hz component
(b) 800 Hz and 900 Hz components
(c) 800 Hz and 100 Hz components
(d) 800 Hz, 900Hz and 100 Hz components
Answer is ( a )
Concept
ExplanationThe frequency at which the aliased signal will be present is given by fm±kfs ;where fm and fs represent message and sampling frequencies respectively with k being an integer. In this example,frequency at 1kHz will get aliased at -0.8(=1+1.8)kHz and 2.8(=1+1.8)kHz.Similarly the signal at -1kHz will get aliased at 0.8(=-1+1.8)kHz and -2.8(=-1-1.8)kHz.After passing through an ideal rectangular LPF with cutoff frequency 1.1kHz, only the component of 0.8kHz remains.
Quantization
 |
| Ask |
An analog signal is band-limited to 4 kHz, sampled at Nyquist rate & the samples are quantized into 4 levels. The quantized levels are assumed to be independent & equally probable. If we transmit two quantized samples per second, the information rate is:
(a) 1 bit/sec
(b) 2 bits/sec
(c) 3 bits/sec
(d) 4 bits/sec
Answer is (d )
Concept
Type Reasoning here
Time Division Multiplexing - TDM
 |
| Ask |
Four messages band limited to W, W, 2W and 3W respectively are to be multiplexed using time division multiplexing. The minimum bandwidth required for transmission of this TDM signal is
(a) W
(b) 3W
(c) 6W
(d) 7W
Answer is (c )
Concept
Minimum bandwidth required for transmission = 2 x (maximum frequency of the message signal)Thus, we have 6W = 2 x (3W)
Frequency Modulation Transmission Bandwidth
 |
| Ask |
A device with input x(t) & output y(t) is characterized by: y(t) = x^2(t). An FM signal with frequency deviation of 90kHz & modulating signal bandwidth of 5kHz is applied to this device. The bandwidth of the output signal is
(a) 370 kHz
(b) 190 kHz
(c) 380 kHz
(d) 95 kHz
Answer is (a)
To find the transmission bandwidth of an FM signal for non-sinusoidal modulation a factor called DEVIATION RATIO must be considered.
Concept
DEVIATION RATIO = Ratio of maximum frequency deviation to the bandwidth of message signal . $$D = \frac{\Delta f}{ W}$$
Thus, Transmission Bandwidth is given by : $$B_T = 2(D+1)W$$
This is the Carson's Rule. There will be a slight modification for single -tone modulated FM Signal case and Sinusoidal FM Signal case.
So, on applying the Above Formula for the given problem:
As the output signal is squared, the frequency deviation is doubled to 180kHz
DEVIATION RATIO = $\frac{180kHz}{5kHz}$ = 36
Bandwidth , $B_T = 2(36+1)5 = 370KHz$
Digital Communication- Pulse Coded Modulation
 |
| Ask |
If the number of bits per sample in a Pulse Coded Modulation (PCM) system is increased from 5 bits to 6 bits,the improvement in signal to quantization noise ratio will be
(a) 3 dB
(b) 6 dB
(c) 2pi dB
(d) 0 dB
Answer is ( b)
Concept
SNRdb = 6.02n+1.76 ; where n is the number of bitsSNRdb(5) = 6.02 x 5 +1.76 = 31.86 dBSNRdb(5) = 6.02 x 6 +1.76 = 37.88 dBSNRdb(6) - SNRdb(5) = 37.88 - 31.86 = 6.02 dBThus we have 6db as the answer
Subscribe to:
Posts (Atom)